Hello World

吞风吻雨葬落日 欺山赶海踏雪径

0%

堆排序

发表于 更新于 分类于

假期补补算法:)

堆数据结构

堆结构图

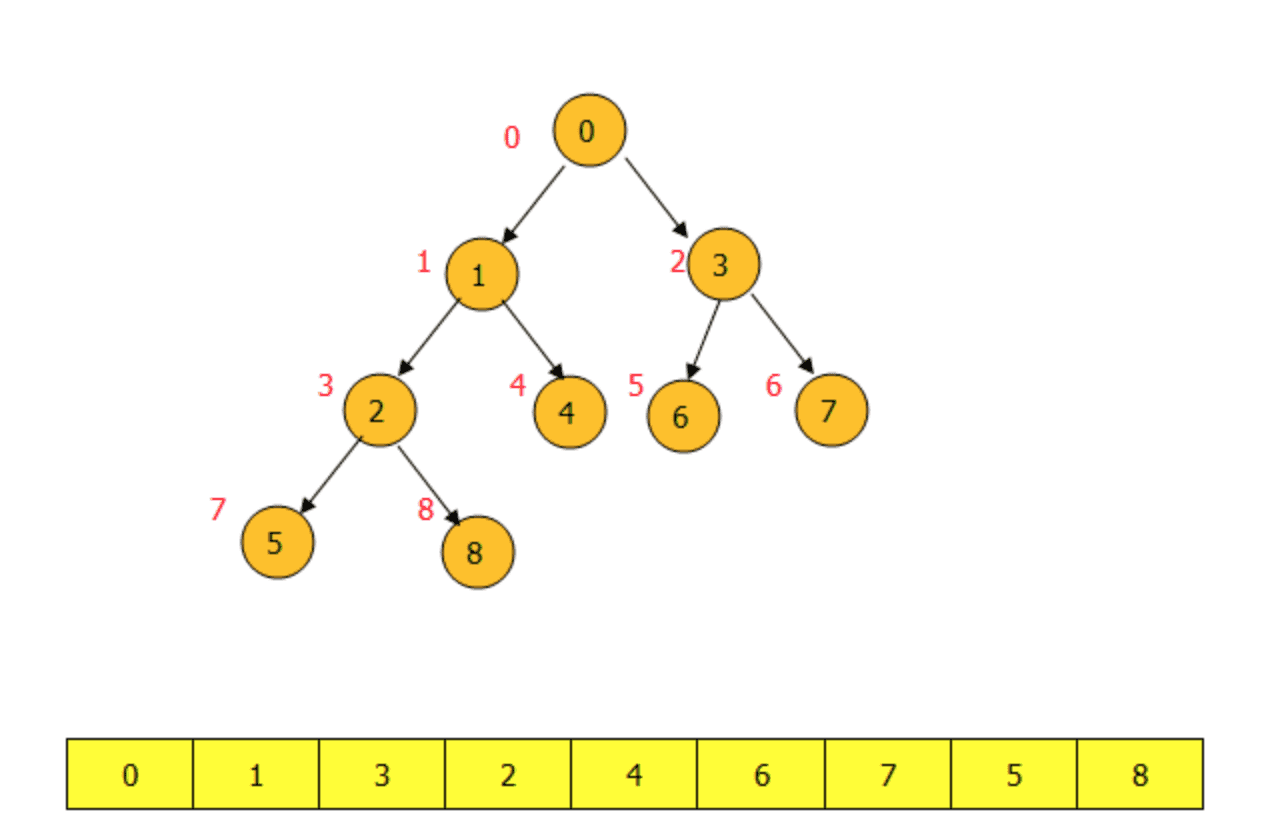
上图表示的是最小堆结构，形式上是一棵完全二叉树，实际存储在内存中的是一个数组，也就是对应下面的数组。树中每一个节点左边红色的值，代表它们在数组中的位置。

堆中节点的关系

父节点与当前节点的下标对应关系为：
当前节点下标为 i 则父节点的下标为（i - 1）/ 2 = parent ，
左孩子节点的下标为：2 * i + 1 = Lchild
右孩子节点的下标为：2 * i + 2 = Rchild

堆的插入

小顶堆为例

① 插人2节点，与其父节点5比较，2比5小交换位置。
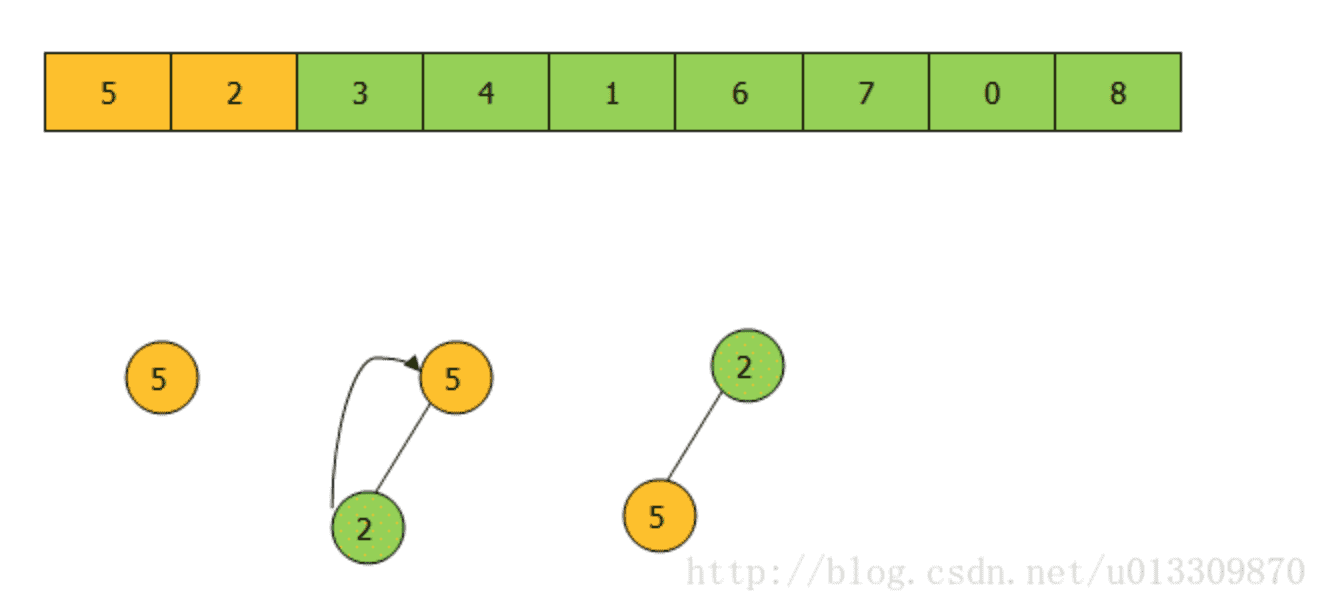
插入第二元素
②插人3节点，与其父节点2比较，3比2大位置不变。
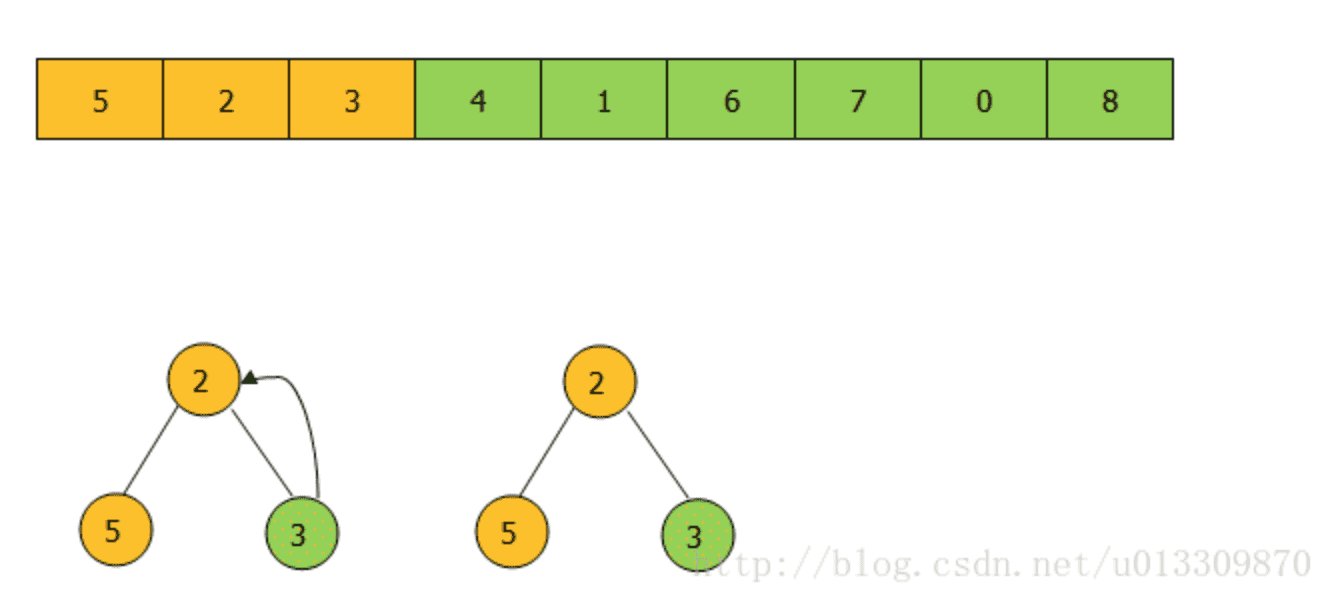
插入第三元素
③插人4节点，与其父节点5比较，4比5小交换4和5的位置，4继续与其父节点2比较，4比2大不变。
插入第四元素

上面插入的过程总结一下：每一个插入的节点放在树的最后一个位置，与其父节点比较，如果比父节点小交换位置，继续与其父节点比较直到比父节点大，或者到了顶节点位置停止。

代码(不包含第一个元素)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//网上摘录的一段
private void siftUp(int k, int arr[]) { 
    //插入的新值key,位置k
    int key=arr[k];
    while (k > 0) {
        //获取父节点下标
        int parent = (k - 1) >>> 1;
        //父节点值e
        int e = arr[parent];
        //父节点值较小，跳出循环
        if(arr[parent]<arr[k])           
            break;
        //否则k节点放入较大值e
        arr[k] = e;
        //父节下标作为新的放入key位置
        k = parent;
    }
    arr[k] = key;
}
//使用Comparator（JDK源码 java.util.PriorityQueue#siftUpUsingComparator ）
private void siftUpUsingComparator(int k, E x) {
    while (k > 0) {
        //定位父节点下标
        int parent = (k - 1) >>> 1;
        //获取父节点数据
        Object e = queue[parent];
        //如果父节点数据较小，退出循环
        if (comparator.compare(x, (E) e) >= 0)
            break;
        //否则 和父节点交换（大值放入子节点中k位置）
        queue[k] = e;
        //k指向父节点下标，继续循环比较其父节点
        k = parent;
    }
    //把x插入下标k
    queue[k] = x;
}

因为插入堆是从底往上的操作因此在api中名称为 siftUp。

堆的删除

删除元素后要对堆进行调整：
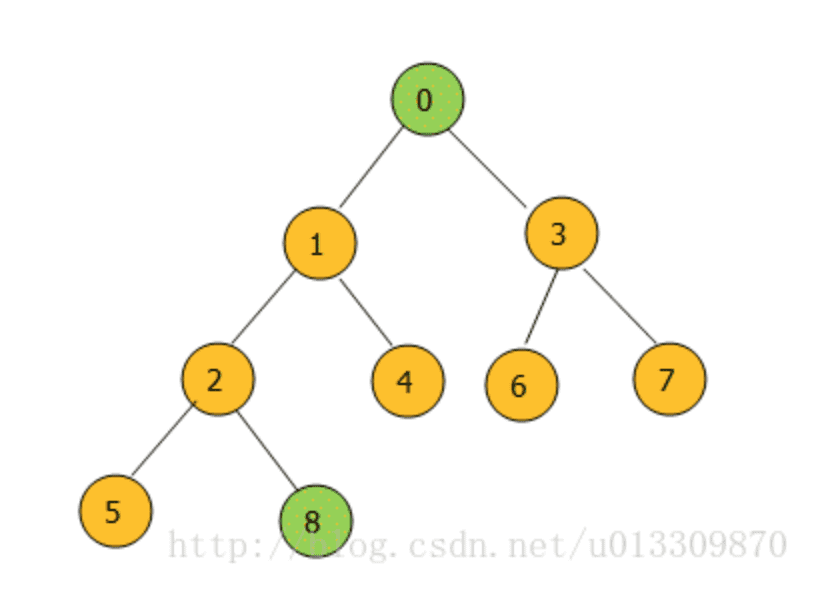
删除堆顶0

堆中每次删除只能删除头节点。也就是数组中的第一个节点。
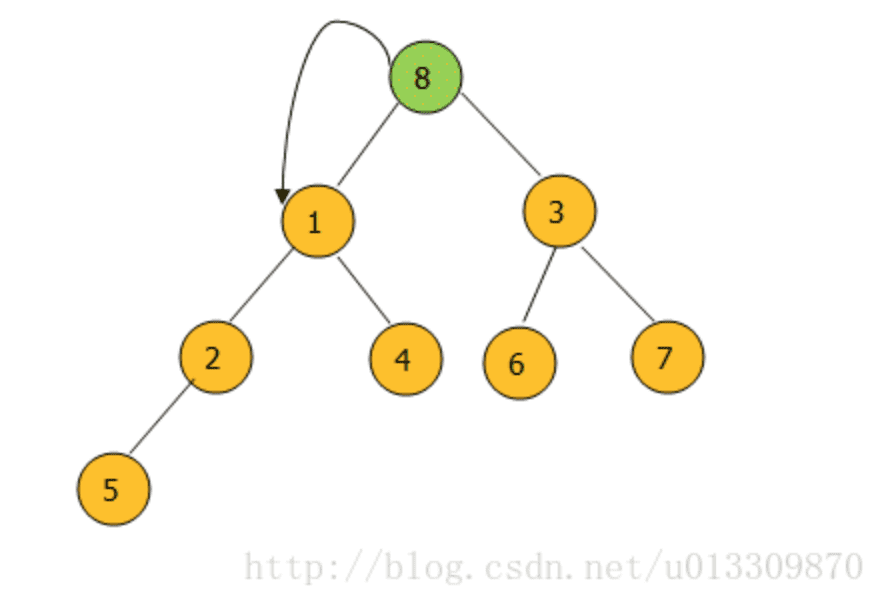
删除后的调整

将最后一个节点替代头节点然后进行调整。
继续向下调整

如果左右子节点中的最小节点比当前节点小就与左右节点的最小节点交换。直到当前节点无子节点，或者当前节点比左右节点小时停止交换。
参见源码 java.util.PriorityQueue#siftDownUsingComparator

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
private void siftDownUsingComparator(int k, E x) {
    //获取所有节点数的一半，用以判断是否是有子节点
    int half = size >>> 1;
    //小于一半还会有子节点
    while (k < half) {
        //左孩子节点下标child
        int child = (k << 1) + 1;
        //左孩子结点值c
        Object c = queue[child];
        //右孩子结点下标right
        int right = child + 1;
        //如果有右子节点，且左子结点值小于右子节点值
        //取出最小的子节点下标child,和最小子节点值c
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        //如果父节点小于等于最小子节点值 跳出循环
        if (comparator.compare(x, (E) c) <= 0)
            break;
        //否则k位置放入最小子节点值
        queue[k] = c;
        //k下标切换成最小子节点下标child继续向下调整
        k = child;
    }
    //k下标位置放入新值x
    queue[k] = x;
}

堆排序

堆排序分为三个过程：

  • 建堆：对数组建堆可以采用从插入堆的方法，从头结点开始不断的进行插入元素向上调整堆。也可以使用堆化的方法从最后节点的父节点开始往前遍历各个父节点做向下调整堆。
  • 堆排序：每次取出堆顶元素，并向下调整堆，重复操作直至堆为空。最终按取出顺序的数据就是有序的。

堆排序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
public class HeapSort implements Sorter{

    //堆排序函数
    @Override
    public int[] sort(int[] arr){
        //最大下标n
        int n = arr.length-1;
        //从最后一个父节点开始往前遍历所有父节点
        for(int i=(n-1)/2;i>=0;i--){
            //构造大顶堆
            //i为最后一个根节点，n为数组最后一个元素的下标
            heapify(arr,i,n);
        }

        //从后往前一个个的递减元素个数（因为最大值放入了最后一个）
        //继续堆化
        for(int i=n;i>0;i--){
            //交换最大值和最后一个元素
            swap(arr,i);
            print(arr,"i="+i);
            //再构造大顶堆（长度在递减）
            heapify(arr,0,i-1);
        }

        return arr;
    }

    // p下标， l最大下标
    //大顶堆堆化
    private void heapify(int[] a,int p,int l){

        int e = a[p];
        int child = p*2+1;
        while(child <= l){
            if(child+1 <= l && a[child+1] > a[child]){
                child = child+1;
            }

            if(e > a[child]){
                break;
            }

            a[p] = a[child];
            p = child;
            child = p*2 + 1;
        }
        a[p] = e ;
    }

    //定义swap函数
    //功能：将跟元素与最后位置的元素交换
    //注意这里的最后是相对最后，是在变化的
    private void swap(int[] arr,int i)
    {
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;
    }


    public static void main(String[] args) {
        HeapSort heapSort = new HeapSort();

        int arr[] = new int[]{9,8,7,6,5,3,4,2,1,0};
        heapSort.sort(arr);
        heapSort.print(arr);
    }
}

堆排序特点

时间复杂度：O(N*logN)

由于建初始堆所需的比较次数较多，所以堆排序不适宜于记录数较少的排序。
堆排序是就地排序，辅助空间为O(1).
堆排序是不稳定的排序方法。（排序的稳定性是指如果在排序的序列中，存在前后相同的两个元素的话，排序前和排序后他们的相对位置不发生变化）

参考

Java堆结构PriorityQueue完全解析
https://blog.csdn.net/u013309870/article/details/71189189

堆排序HeapSort（Java）
https://blog.csdn.net/u013309870/article/details/68578011